读书笔记——视觉SLAM十四讲(2)
初认SLAM
三维空间刚体运动
旋转矩阵(冗余度高)
旋转矩阵
两个坐标系间的运动被称为刚体运动,(一个旋转+一个平移)这个过程被称为欧氏变换
故可以得出 $$ 矩阵 R 描述旋转本身 -> 旋转矩阵(方向矩阵) $$ 因此欧氏变化用数学表示: $$ a’ = Ra + t $$ 或者表示为: $$ a_1 = R_{12} a_2 + t_{12} $$
$$ R_{12} => 把坐标系2的坐标变换到坐标系1 $$
$$ t_{12} => 从1到2的向量(坐标系1原点指向坐标系2原点的向量) $$
“求我的当前坐标“可以表示为: $$ t_{wc} $$
变换矩阵
为了让多次移动具有线性,引入齐次坐标与变换矩阵,从而将旋转平移写在同一矩阵中,创建线性关系,其中T被称为变换矩阵 [ \(\left\{ \begin{matrix} a' \\ 1 \end{matrix} \right\} = \left\{ \begin{matrix} R & t \\ 0^T & 1 \end{matrix} \right\} * \left\{ \begin{matrix} a \\ 1 \end{matrix} \right\} = T \left\{ \begin{matrix} a \\ 1 \end{matrix} \right\}\) ] 总的来看,旋转矩阵和变换矩阵的特点如下:
| 数学表示 | 名称 | |
|---|---|---|
| T_{a} | 齐次坐标 | 特殊欧氏群SE(3) |
| R_{a} | 非齐次坐标 | 特殊正交群SO(3) |
Eigen
Eigen是一个开源的C++库,主要用于高效的线性代数运算,特别是矩阵和向量的操作。它提供了丰富的功能,包括矩阵的乘法、求逆、特征值计算等,支持稠密矩阵和稀疏矩阵,并且可以与多线程、并行计算兼容。
Eigen以其简洁的接口、良好的性能和高效的内存管理著称,广泛应用于计算机视觉、机器学习、物理仿真等领域。它是跨平台的,支持Windows、Linux和macOS等操作系统。
旋转向量和欧拉角
旋转向量
用矩阵表示旋转的缺点:1、表达式冗余大。2、表达形式有限制,要求必须是正交阵。
可以用三维向量表示旋转,六维向量表示变换(1个旋转轴 + 1个旋转角) $$ 旋转轴为向量n,旋转角为\theta,那么可以用 \theta n 描述旋转 $$
$$ 且旋转轴上的向量在旋转后不发生改变,即Rn = n $$
欧拉角(更直观的描述旋转,但存在“万向锁”问题——奇异性)
| 转角 | 对应关系 |
|---|---|
| 绕物体的Z轴 | 偏航yaw |
| 绕旋转之后的Y轴 | 俯仰pitch |
| 绕旋转之后的X轴 | 滚转roll |
四元数(提供不带奇异性的描述,复杂性突出)
一般来说,可以用单位负数描述二维旋转,同理,可以用单位四元数描述三维旋转 $$ q(w,x,y,z)=w+xi+yj+zk \tag{1} $$
$$
q = q_0 +q_1i+q_2j+q_3k={ s,v }^T \tag{2}
其中s=q_0称为实部,v=[ q_1,q_2,q_3 ]^T称为虚部
$$
那么,如何用四元数表示旋转呢
$$
p = [0,x,y,z]^T = [0,v]^T
p’=Rp
p’ = qpq^{-1}
$$
相当于把四元数的3个虚部与空间中的3个实部相对应
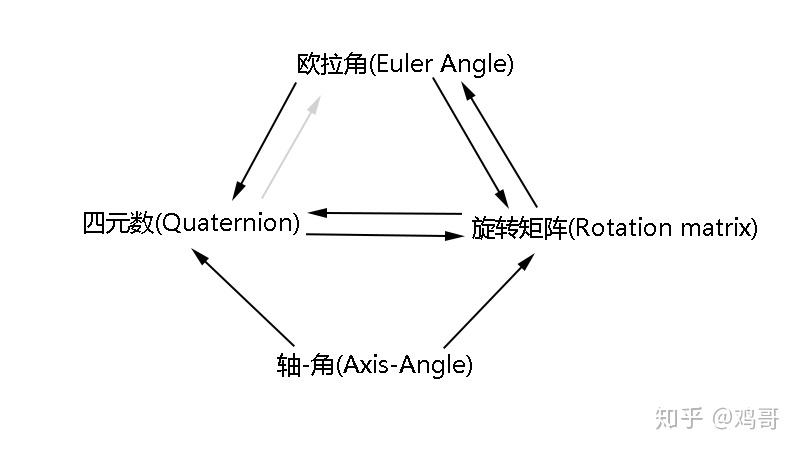
四元数与其他旋转的关系
$$
q = [s,v]^T
$$
四元数到旋转矩阵
[
\(R = vv^T + s^2I+2sv^{}+(V^{})2 \\
R =
\left\{
\begin{matrix}
1-2y^2-2z^2 & 2xy-2zw & 2xz+2yw \\
2xy+2zw & 1-2x^2-2z^2 & 2yz-2xw \\
2xz-2yw & 2yz+2xw & 1-2x^2-2y^2
\end{matrix}
\right\} \tag{2}\)
]
四元数到旋转向量
$$
\theta = 2\arccos q_0
[n,n,n]^T = [q,q,q]^T/ \sin(\theta / 2)
$$
参考资料
https://zhuanlan.zhihu.com/p/45404840